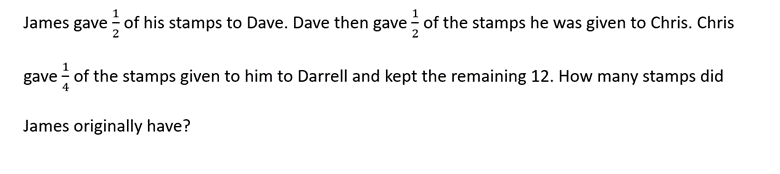|
Students, Parents, Teachers! You can request to have a question answered in video form.
|
Welcome, Steps to Success in Mathematics. |
|
The video discusses how to solve a math problem involving unequal sharing and using diagrams to represent the problem.
|
The video explains how to calculate the price of a jug and a glass given a specific scenario, and the answer is that the difference between the two prices is $4.
|
|
The video explains how James cuts a piece of wood into multiple pieces, each measuring 65 centimeters long
|
The video explains how to solve a math problem involving distance and fractions, with the answer being 128 kilometers.
|
Three children, John, Benny, and Larry, receive different amounts of money: John gets $100, Benny gets $80, and Larry gets $130.
|
|
The video explains how to determine the values of a triangle, trapezium, and square by using association and substituting techniques.
|
The video explains a strategy for solving a math problem involving the cost of sharpeners and rulers and determines that the cost of one sharpener and one ruler.
|
The video explains how to solve a problem involving the calculation of the cost of specific items and the total cost of those items purchased by two individuals.
|
|
The video explains how to calculate the cost of a mini tablet based on the cost of a tablet and mini tablet bundle.
|
The video discusses the strategy of guess and check to determine the number of games lost in a scenario where there are a total of 10 points scored based on wins, draws, and losses.
|
The video provides a strategy for solving a math problem involving the purchase of donuts and cupcakes, using a table and guess-and-check method.
|
|
|
The video explains how to solve a math problem using fractions and a diagram, ultimately determining the total number of bulbs a company bought.
|
The video teaches how to solve a measurement problem involving the area of a kitchen floor and the cost of tiles, with the final answer being $4500.
|
|
The video demonstrates how to solve a math problem involving fractions by using strategies such as making a diagram, bar modeling, and working backwards, ultimately arriving at the answer of 280 cupcakes in total.
|
The video discusses a strategy for solving a money problem through guessing and checking using an organized table, with the final answer being that Tara bought 12 pies.
|
The video provides a step-by-step solution to a math problem involving profit and loss, using strategies such as reading slowly to understand, setting up equations, and diagramming fractions.
|
|
The video explains how to solve a fraction question involving the distribution of stamps between multiple individuals.
The video explains how to solve a math problem involving the distribution of oranges between two people, and ultimately calculates the number of oranges Rudy had at the beginning.
|
Most Recent Videoes Posted
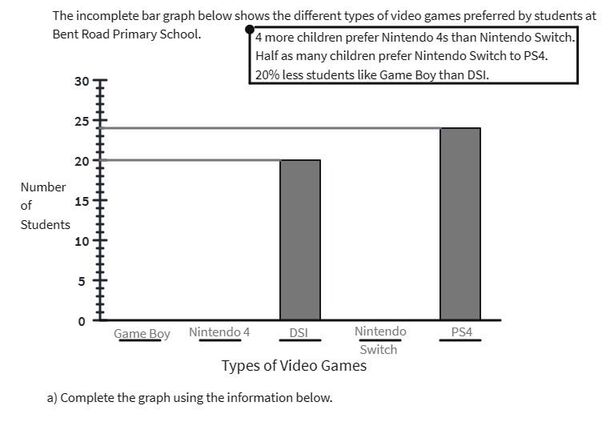
The video explains how to complete a bar graph using given information and clues.
The video explains how to calculate average earnings for a taxi driver and demonstrates the concept of average using bar graphs, while also providing possible sets of values for Saturday and Sunday earnings.
The video demonstrates how to solve math problems involving mean by using given clues to calculate missing numbers.
The video discusses a math problem involving three students selling pens, where it is determined how many pens they sold altogether.
The video provides a step-by-step explanation of how to solve a time calculation problem involving converting minutes to hours, creating number bonds, and using a timeline.
|
Student Problems
|
Topic: Fraction Problems
Strategy: Drawing diagrams
In some fraction problems the whole is not given. A common mistake you might make is to multiply the fraction by any of the numbers in your problem. Don't be too quick to multiply. I suggest drawing a diagram of the fraction you are unsure of, then use it later. Take a look at these questions to see how drawing helps. |
|
|
Topic: Proft and Loss
Skill: Multiplying Decimals. Remember that profit or loss is a change in the original price of an item.
|
|
|
Topic: Interpreting Remainders in Division Problems
Strategy: Division comes in two flavours
|
What type of division is shown in this question?
a) Sharing b) Grouping 
|
|
Topic: Number Patterns
Skill: Multiplying Decimals. Writing a number pattern requires 3 steps.
|
Click to set custom HTML
|
|
Topic: Problems involving Average
Strategy: It's important to remember that averages can change by either increasing it or decreasing it. Here is a look at an example question.
|
NB: There is a slight error in the problem (294 should be 304. )
Ron did 2 more tests, so his mean changed from 76 to 80. Let's take a look. 
|
|
Topic: Area Problems
Skill: Multiplying Decimals. Let's take a look. |
|
|
Topic: Associative Law of Addition
Strategy: It's important to remember the basic facts about common intervals. I explain them in this video.
|
|
|
Topic: Unequal Sharing
Strategy: Draw a diagram to explain the comparison statements. In this question there is a change that results in an unequally shared number of oranges between the two children. Let's take a look. |
Hi Lisa, I hope this helps improve your understanding of bar models 
Changing ONE word in this question could make a BIG difference in the diagrams we draw. Let's take a look.
Hi Annis, I hope this video clears up any confusion your child is having. Strategy: In the past I would have mentioned "If a clue is not yet useful, rest it and move on." This is still an excellent suggestion but be aware of comparison statements like the one found in this problem.
|
|
Topic: Common Intervals
Let's learn about common intervals Strategy: It's important to remember the basic facts about common intervals. I explain them in this video.
|
|
|
Topic: Time
Strategy: Many time questions can be solved using a timeline.
In this question we can use the timeline to add or subtract time mentally. Remember students you must learn the skill of converting minutes to hours and hours to minutes. |
Hi Anjanique, I totally understand why this question could be a bit confusing. Here are tips for solving it.
|
|
Topic: Bar Graphs
Top Tip: If a clue is not yet useful, rest it and move on. Be sure to come back to it when you can. In this question students are given clues in order to complete a graph. Here are some things to pay attention to:
|
|
Vertical Divider
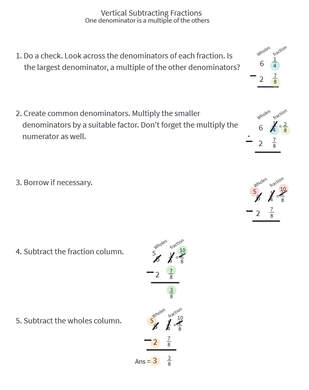
Thank you, Jalon, for requesting the topic! Subtracting fractions can get tricky. |
|
Hi Talya and Zariah! Let's see the distributive law of multiplication in ACTION! Topic: Distributing Multiplication
Strategy: We can share one of the factors in a multiplication problem into an addition bond This creates smaller multiplication problems that add to give the original product. 20 x 13 = (20 x 10) + (20 x 3) |
In this third video I explain how to calculate unknown amounts using the distributive law of multiplication.
Understanding distributive law using area/arrays
In this video I recap the use of the distributive law as an algorithm.
In this third video I explain how to calculate unknown amounts using the distributive law of multiplication.
|
|
Topic: Fractions (Line Models)
Strategy: Represent fractions on a number line. Learners me be allowed to encounter different ways of representing fractions: linear, area and set models. Too often, teachers focus on area models using rectangles or circles to describe fractions. |
|